Cubo. Ortoedro. Unidades de volumen

Observemos un dado. Si prescindimos de la materia de que está hecho, de su color, etc., constituye un cuerpo geométrico denominado cubo.

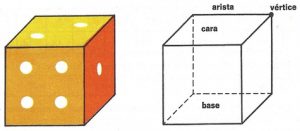-Está limitado por seis cuadrados iguales, llamados caras.

–Cada uno de los lados comunes a dos de estos cuadrados es una arista del cubo.

–Los puntos donde concurren tres aristas son los vértices del cubo.

¿Cuántas caras, aristas y vértices tiene el cubo? El cubo tiene seis caras cuadradas, doce aristas iguales y ocho vértices.

CONSTRUCCIÓN DEL CUBO
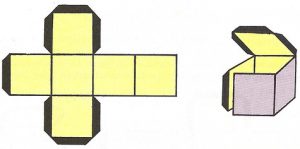Dibujemos en una cartulina las seis caras del cubo tal como indica la figura. Doblemos después por las aristas y peguemos las pestañas señaladas en color oscuro.

EL ORTOEDRO. DEFINICIÓN Y PROPIEDADES
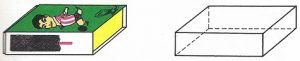
Observemos una caja de cerillas. Prescindiendo de la materia de que está hecha y atendiendo solamente a la forma, constituye un cuerpo geométrico llamado ortoedro.

Está limitado por seis rectángulos, dos a dos iguales y paralelos, llamados caras.

¿Cuántas aristas y vértices tiene? Como el cubo, el ortoedro tiene seis caras, doce aristas y ocho vértices.

Hay tres grupos de cuatro aristas iguales entre sí.

La longitud común de las cuatro aristas de uno de estos grupos se llama una dimensión del ortoedro. Así, este tiene tres dimensiones: largo, ancho y alto.

Si se supone que el ortoedro reposa sobre el suelo, la cara en contacto con el mismo se llama base, así como la cara opuesta. Las restantes son las caras laterales.

El cubo es un ortoedro cuyas tres dimensiones son iguales.

CONSTRUCCIÓN DEL ORTOEDRO
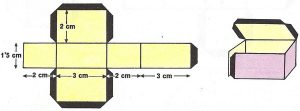Supongamos que queremos construir un ortoedro de 3 cm de largo, 2 cm de ancho y 1,5 cm de alto. Dibujemos en una cartulina sus seis caras, como se indica en la figura. Doblemos después por las aristas y peguemos las pestañas señaladas en color oscuro.

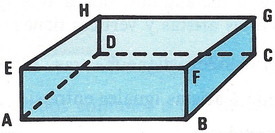
Ejercicio: Dibuja un ortoedro y nombra: a) vértices adyacentes; b) vértices opuestos; c) aristas perpendiculares; d) aristas paralelas; e) aristas que se cruzan; f) caras paralelas; g) caras perpendiculares.

Solución:

a) A y B, A y E, C y G, F y G.
b) A y G, B y H, E y C, D y F.
c) AE y AB, BC y CD, DH y EH…
d) AB, EF y DC; BC, FG, EH y AD; AE, BF, CG y DH.
e) AE y HG, BC y DH…
f) ABCD y EFGH; ABEF y DCHG; ADEH y BCFG.
g) ADEF y EFHG; BCFE y ABCD…

PARALELEPÍPEDOS
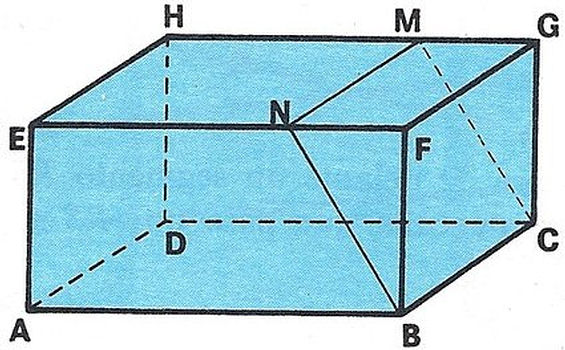
Construye un ortoedro ABCDEFGH, de plastilina, y colócalo sobre la mesa:

En la cara superior, EFGH, señala un segmento MN paralelo a uno de los lados menores (ancho). Da un corte según un plano no paralelo a la cara AEHD que pase por MN y por BC.

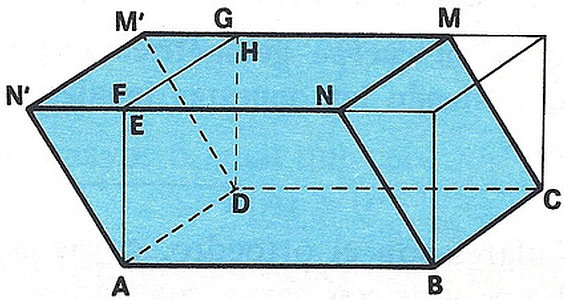
Coloca la cuña obtenida de modo que la cara BCFG coincida con la ADHE. Obtenemos así un cuerpo geométrico ABCDMNM’N’, llamado paralelepípedo. Sus dos bases son rectángulos, pero las cuatro caras laterales son paralelogramos.

Ejercicio: A partir del paralelepípedo anterior ABCDMNM’N’, ¿cómo construirías otro con las cuatro caras laterales paralelogramos?

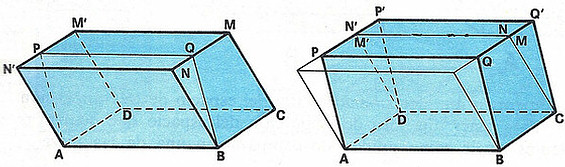
Solución: Se traza en la base superior un segmento PQ paralelo a uno de los lados mayores M’M (largo).

Damos un corte en forma de cuña que pase por PQ y AB. Unimos la cuña cortada de modo que la cara ABN’N coincida con DCM’M.

Ejercicio: A partir del paralelepípedo ABCDPQQ’P’, ¿cómo construirías otro con las seis caras paralelogramos?

Solución: Bastará trazar en la cara de delante un segmento RS paralelo a AP (alto) y dar un corte en forma de cuña que pase por RS y DP’.

En general:

El paralelepípedo es un cuerpo geométrico con seis caras, que son paralelogramos, siendo las opuestas iguales y pertenecientes a planos paralelos.

Dos casos particulares son el ortoedro, cuyas seis caras son rectángulos y el cubo con las seis caras, cuadrados.

VOLUMEN
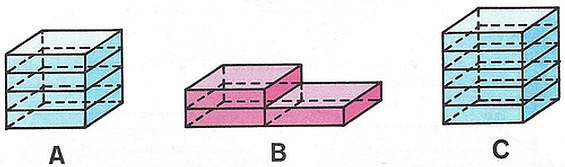
Un juego de rompecabezas se compone de muchas piezas iguales. Con ellas armamos distintos cuerpos: A, B y C: …

…que ocupan una determinada parte del espacio de tres dimensiones.

Para tener una idea de la porción del espacio que llenan, podemos elegir como unidad de comparación una de las piezas del rompecabezas. De este modo, a cada cuerpo le podemos asociar un número que indica la extensión de espacio que ocupa:

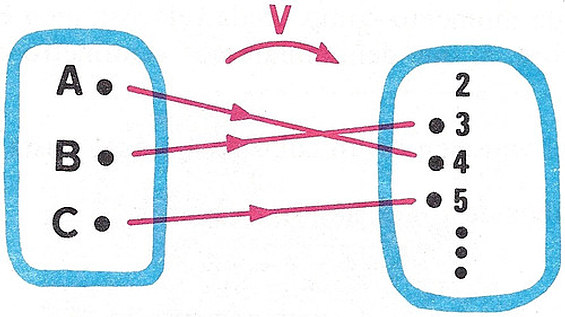
A este número se llama volumen. Así:

V(A) = 4
V(B) = 3
V(C) = 5

Podemos deducir inmediatamente que el volumen tiene las siguientes propiedades:

1.ª)Es un número mayor o igual que cero:
V(A) ≥ 0

2.ª)Si dos cuerpos son iguales, tienen igual volumen:
A = B ⇒ V(A) = V(B)

3.ª)Si juntamos los cuerpos A y B se forma otro cuerpo F, cuyo volumen es la suma de los volúmenes de A y B.

Es decir, V(A ∪ B) = V(A) + V(B) = V(F)

Podemos resumir todo lo expuesto en la siguiente definición: Volumen de un cuerpo es la medida que expresa la porción del espacio de tres dimensiones que ocupa dicho cuerpo.

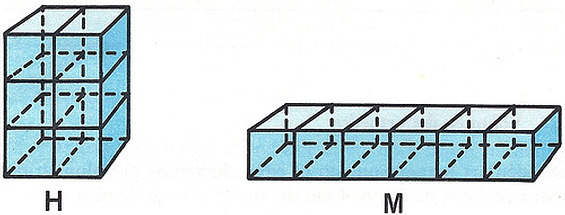
Dos cuerpos, aunque no sean iguales, si tienen igual volumen, se llaman equivalentes. Ejemplo: el cuerpo H y M son equivalentes.

VOLUMEN DEL CUBO
Tomemos de momento como unidad de volumen el de un cubo de 1 cm de arista, al que denominaremos centímetro cúbico. Se escribe cm³.

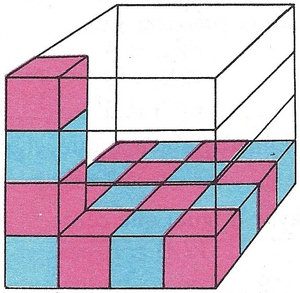Hallemos el volumen de un cubo de 4 cm de arista.

¿Cuántos cubos de 1 cm³ hay en cada capa?
4 x 4 = 16

¿Cuántas capas idénticas a la anterior llena el cubo?
4 capas.

¿Cuánto es el máximo número de cubos de 1 cm³ que cabe en el cubo?
16 x 4 = (4 x 4) x 4 = 64 cm³

Por tanto:

Volumen del cubo = arista x arista x arista = a³

VOLUMEN DEL ORTOEDRO
De idéntica manera que en el cubo, hallemos el volumen de un ortoedro de 5 cm de largo, 4 cm de ancho y 3 cm de alto.

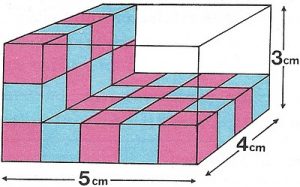¿Cuántos cubos de 1 cm³ se pueden colocar sobre el fondo del ortoedro?
5 x 4 = 20

¿Cuántas capas análogas a la anterior pueden meterse en el ortoedro?
3 capas.

¿Cuál es el máximo número de cubos de 1 cm³ que caben en el ortoedro?
20 x 3 = 5 x 4 x 3 = 60 cm³

Volumen del ortoedro = largo x ancho x alto = l • a • h

Ejercicio: Una maleta tiene las siguientes dimensiones: 75,4 cm de largo, 51,3 cm de ancho y 24 cm de alto. Halla su volumen en centímetros cúbicos.

Solución:

V = l • a • h = 75,4 x 51,3 x 24 = 92.832,48 cm³

MEDIDAS DE VOLUMEN
En el apartado anterior vimos que el volumen es un número que expresa la medida de la extensión de los cuerpos en el espacio de tres dimensiones.

Ahora bien, el valor de esta medida depende del cuerpo que elijamos como referencia para comparar los demás cuerpos. El volumen de dicho cuerpo sirve de unidad.

A continuación estudiaremos las unidades de volumen más utilizadas y las relaciones que se establecen entre ellas.

UNIDADES DE VOLUMEN
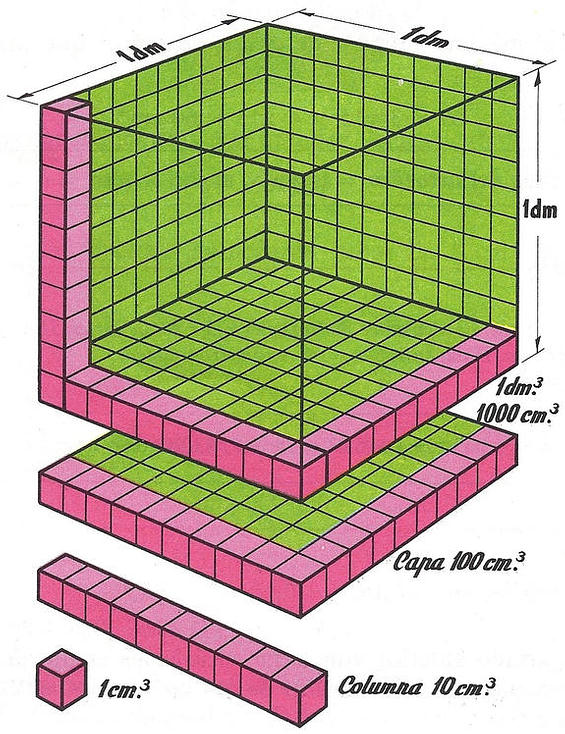
Fíjate en la figura que representa un cubo de 1 dm de arista. Su volumen lo elegimos como unidad y lo denominaremos decímetro cúbico. Se escribe dm³.

-El decímetro cúbico puede dividirse en 10 capas, compuesta de 10 columnas de 10 cm³ cada una.

1 dm³ = 10 x 10 x 10 cm³ = 1.000 cm³

-Del mismo modo, el centímetro cúbico (cm³) se puede dividir en 1.000 milímetros cúbicos (mm³):

1 cm³ = 10 x 10 x 10 mm³ = 1.000 mm³

La unidad fundamental de volumen es el metro cúbico (m³), que es el volumen de un cubo de 1 m de arista:

1 m³ = 1.000 dm³ = 1.000.000 cm³ = 1.000.000.000 mm³

Una unidad de un orden es 1.000 veces menor que la del orden inmediato superior.

1 dm³ = 0,001 m³ (milésima parte del m³)
1 cm³ = 0,000001 m³ (millonésima parte del m³)
1 mm³ = 0,000000001 m³ (milmillonésima parte del m³)

Se necesita un grupo de tres cifras para representar cada unidad.

CAMBIO DE UNIDAD
Sea, por ejemplo, la cantidad 37,6254 m³. Para expresarla en dm³, cm³ o mm³, basta multiplicarlo por 1.000, 1.000.000, 1.000.000.000, ya que:

1 m³ = 1.000 dm³ = 1.000.000 cm³ = 1.000.000.000 mm³

Por tanto,
37,6254 m³ = 37.625,4 dm³ = 37.625.400 cm³ = etc.

Al contrario, para expresar la cantidad dada en unidades de orden superior, habrá que dividir por 1.000, 1.000.000, etc. Así:

5.023.715,670 cm³ = 5.023,715670 dm³ = 5,023715670 m³

Ejercicio: Convierte en cm³: la décima de m³; 10 dm³; 7.250 mm³; la centésima de dm³; ½ m³; ¼ dm³.

Solución:

0,1 m³ = 100.000 cm³
10 dm³ = 10.000 cm³
7.250 mm³ = 7,250 cm³
0,01 dm³ = 10 cm³
½ m³ = 500.000 cm³
¼ dm³ = 250 cm³

REDUCCIÓN DE COMPLEJOS A INCOMPLEJOS Y VICEVERSA
Supongamos que al medir el volumen de una habitación se obtenga el número complejo 372 m³, 5 dm³, 43 cm³. Pero como 372 m³ son 372.000.000 cm³ y 5 dm³ son 5.000 cm³, el volumen de la habitación será:

372.000.000 + 5.000 + 43 = 372.005.043 cm³

Ejercicio: Escribe el número complejo 52 dm³, 3 cm³, 608 mm³ en mm³.

Solución:

52 dm³, 3 cm³, 608 mm³ = 52.003.608 mm³

Recíprocamente, si tenemos el volumen siguiente: 92.832,480 cm³ podemos escribirlo como 92 dm³ 832 cm³ 480 mm³. Es decir:

92.832,480 cm³ = 92 dm³ + 832 cm³ + 480 mm³

Ejercicio: Pasar a complejo el número 5.023.715,67 cm³.

Solución:

5.023.715,67 cm³ = 5 m³ 23 dm³ 715 cm³ 670 mm³

•Cómo saber si he sido secuestrado por alienígenas. Pérdida de tiempo, terror irracional, alteraciones del sueño, hemorragias... Los investigadores de la abducción dicen que estos indicios son comunes en personas presuntamente secuestradas por alienígenas. Pero, cuidado, estos síntomas pueden indicar también problemas terrenos que requieran de atención médica.

•El viejo hombre de Shropshire. Uno de los casos más aceptados de longevidad inusual, incluso entre la comunidad científica, fue el del británico Thomas Parr, que decía tener 152 años en 1635. Considerada hoy día un mito, está enterrado en el Rincón de los Poetas de la Abadía de Westminster, al lado nada menos que de Shakespeare, Byron y Milton.

•El Triángulo de las Bermudas. Las desapariciones en el mar han sido numerosas y aun los casos no resueltos son generalmente explicables. Pero si existe un lugar donde las condiciones en que han sucedido estos dramas permanecen aún en la oscuridad, ese lugar es sin duda una extensa área geográfica situada entre las islas Bermudas, Puerto Rico y Florida.

•Experiencia cercana a la muerte. Sensación de atravesar un túnel, experiencia extracorpórea, visiones de luz, encuentros con personajes espirituales y amistades o parientes difuntos... Estos son algunos rasgos comunes de las ECM. Quienes lo han experimentado pierden el miedo a la muerte, se toman las cosas con más calma, serenidad y filosofía, son más felices.

MUY IMPORTANTE: Revista CAOS se define a sí misma como una web solidaria, es por ello que desinteresadamente deseamos lanzar una campaña de concienciación de nuestros corazones. Observamos con desasosiego que estamos perdiendo humanidad. Salvo en situaciones muy concretas de gran resonancia mediática, cada vez nos cuesta más mostrar afecto por el desconocido, ofrecer ayuda si a cambio no vamos a sacar una contrapartida por pequeña que esta sea… y resulta intolerable. No podemos hacer de este mundo algo tan horrible, tan egoísta, tan frío, tan falto de vida, por ello animamos a todo aquel que visita nuestra página a una reflexión sincera que le empuje a activarse y participar en alguna asociación de ámbito local que ayude a los más necesitados, a los faltos de recursos, ancianos, niños, discapacitados, enfermos terminales, que se preocupe por el cuidado del medioambiente, en contra de la crueldad con los animales… Y no hablamos sólo de dinero: dona ropa, sangre… levanta la vista, deja el teléfono móvil por un rato y ofrece tu tiempo, amistad, apego, conocimientos profesionales… No hacemos publicidad de ninguna entidad en concreto para que cada cual escoja aquella que le haga sentir más a gusto y de ese modo asuma la causa ajena como propia. Estamos seguros que si cada uno de nosotros pone un pequeño granito de arena en su entorno, todos juntos, por extensión, haremos de este planeta un lugar mejor, un rincón del cosmos donde realmente merezca la pena vivir; y de paso erradiquemos ese mal humor perpetuo, esa falta de educación y ausencia de empatía que inunda las calles de nuestros barrios y ciudades. En nombre de todas esas personas a las que a diario regalas lo mejor de ti mismo y la mayor de tus sonrisas, de corazón: muchas gracias.