Conjuntos

En forma esquemática y resumida, vamos a intentar aclarar algunos conceptos importantes sobre el tema:

PRODUCTO CARTESIANO DE DOS CONJUNTOS
Sean los conjuntos A={1,2,3} y B={a,b,c}.

Se llama producto cartesiano A x B, al conjunto de todos los posibles pares de elementos ordenados.

O sea:
A x B={(1,a),(1,b),(1,c),(2,a),(2,b),(2,c),(3,a),(3,b),(3,c)}

-todos los posibles: Cada elemento del primer conjunto A, forma parte con todos los del segundo B y al contrario.

-pares de elementos: Los elementos del producto están formados por dos elementos en forma de par: primera componente y segunda componente.

-ordenados: La primera componente debe ser del primer conjunto y la segunda componente del segundo conjunto.

En general:
A x B={(x,y)/x∈A; y∈B}

RELACIÓN BINARIA. PROPIEDADES
Consideramos el conjunto A={gato, perro, sardina}.
Establecemos la relación de “vivir en el mismo medio”.

Decimos que:
Una relación binaria es una ley o criterio establecido entre los elementos de un mismo conjunto.

Las relaciones binarias se representan por:

–diagrama sagital:

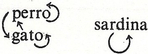
-pares: subconjunto del producto cartesiano A x A. Se llama grafo de la relación:

G={(p,p),(p,g),(g,p),(g,g),(s,s)}

Las relaciones binarias pueden tener varias propiedades:

1)Reflexiva: “Todo elemento se relaciona consigo mismo”.
aRa, ∀a∈A

2)Simétrica: “Si un elemento a está relacionado con otro b, entonces b se relaciona con a”.
Si aRb ⇒ bRa

3)Antisimétrica: “Si un elemento a está relacionado con otro distinto b, entonces b no se relaciona con a”.

4)Transitiva: “Si a se relaciona con b y b se relaciona con c, entonces a se relaciona con c”.
Si aRb y bRc ⇒ aRc

RELACIÓN DE EQUIVALENCIA
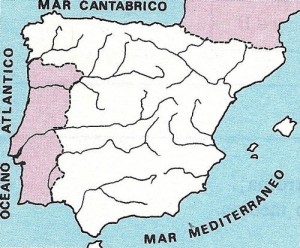En el conjunto A de los ríos de España establecemos la relación binaria de “desembocar en el mismo mar que”:

1)Reflexiva: Todo río desemboca en el mismo mar que él mismo.

2)Simétrica: Si un río “a” desemboca en el mismo mar que otro “b”, este “b” desemboca en el mismo mar que “a”.

3)Transitiva: Si “a” y “b” desembocan en el mismo mar y a su vez “b” y “c” desembocan en el mismo mar, es evidente que “a” y “c” desembocan en el mismo mar.

Toda relación binaria que cumple las propiedades reflexiva, simétrica y transitiva es una relación de equivalencia.

-Toda relación binaria de equivalencia divide al conjunto en varios subconjuntos o clases.

Cada subconjunto se llama clase de equivalencia. Son disjuntos (no hay ningún río que desemboque en dos mares a la vez).

-Al conjunto nuevo formado al tomar como elementos las clases anteriores, se llama conjunto cociente. En el ejemplo, el conjunto cociente será:
A/R={vert. atlántica, vert. mediterránea, vert. cantábrica}

RELACIÓN DE ORDEN
Dado el conjunto N de los números naturales establecemos la relación “ser múltiplo de”.

Esta relación es:

1)Reflexiva: Todo número es múltiplo de sí mismo, a=a ∀a∈N.

2)Antisimétrica: Si un número a es múltiplo de otro b y b no es múltiplo de a, entonces a es distinto de b.

3)Transitiva: Si a es múltiplo de b y b es múltiplo de c entonces a es múltiplo de c.

Toda relación binaria que cumple las propiedades reflexiva, antisimétrica y transitiva es una relación de orden.

Las relaciones de orden pueden ser:

-Totales: Si todos los elementos se relacionan. O aRb o bRa.

-Parciales: Hay elementos que se relacionan y otros que no se relacionan.

El conjunto se dirá totalmente ordenado o parcialmente ordenado, según el tipo de relación de orden introducido.

DEFINICIÓN DE LOS NÚMEROS NATURALES (N)
Consideremos la relación de coordinabilidad entre conjuntos. Esta relación tiene las propiedades:

1)Reflexiva: Cualquier conjunto es coordinable consigo mismo.

2)Simétrica: Si un conjunto A es coordinable con otro B, este es coordinable con A.

3)Transitiva: Si un conjunto A es coordinable con otro B y este es coordinable con un tercero C, entonces A es coordinable con C.

Por tanto, esta relación es de equivalencia. La relación de coordinabilidad clasifica los conjuntos en clases de equivalencia. En cada una de las clases están todos los conjuntos que son coordinables entre sí, es decir, que tienen el mismo número de elementos.

A cada clase de equivalencia se designa por un nombre o símbolo y se denomina número natural.

El conjunto {0,1,2,3,4, …}=N es el conjunto de los números naturales.

Contar un conjunto es establecer una aplicación biyectiva entre dicho conjunto y un subconjunto de los números naturales.

CORRESPONDENCIA
Correspondencia entre dos conjuntos A y B es todo criterio que permite asignar a elementos del primer conjunto A, elementos del segundo conjunto B.

Las correspondencias se simbolizan por letras minúsculas f, g, h, etc.

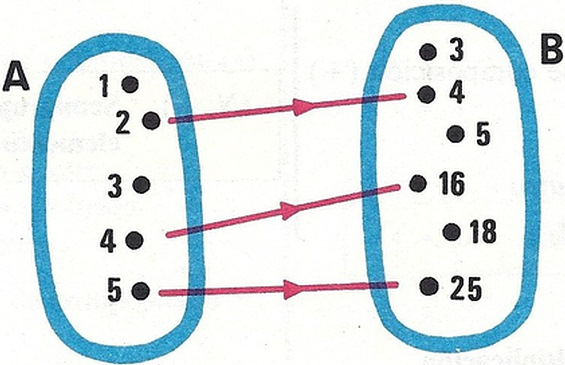
Una correspondencia entre los conjuntos A={1,2,3,4,5} y B={3,4,5,16,18,25} puede ser la representada en el diagrama siguiente:

Se llama grafo de la correspondencia al conjunto de pares ordenados del producto cartesiano A x B que cumplen el criterio dado.

Así, el grafo de la correspondencia representada anteriormente será:

CONJUNTOS INICIAL, FINAL, ORIGEN E IMAGEN
En toda correspondencia entre dos conjuntos A y B se pueden considerar los siguientes conjuntos:

-Conjunto inicial: Es el primer conjunto A.
-Conjunto final: Es el segundo conjunto B.
-Conjunto origen: Es el conjunto de elementos de A que tienen imagen en B [Or(f) = Dom(f)].
-Conjunto imagen: Es el conjunto de elementos de B que tienen antiimagen en el A [Im(f)].

En la correspondencia establecida en el ejemplo anterior se pueden considerar los conjuntos:

-Conjunto inicial: A={1,2,3,4,5}.
-Conjunto final: B={3,4,5,16,18,25}.
-Conjunto origen: Or(f)={2,4,5}.
-Conjunto imagen: Im(f)={4,16,25}.

FUNCIONES Y APLICACIONES
Aplicación de A en B es una correspondencia tal que todo elemento del conjunto inicial A tiene una imagen y sólo una en el conjunto final B.

Las aplicaciones también se llaman funciones uniformes.

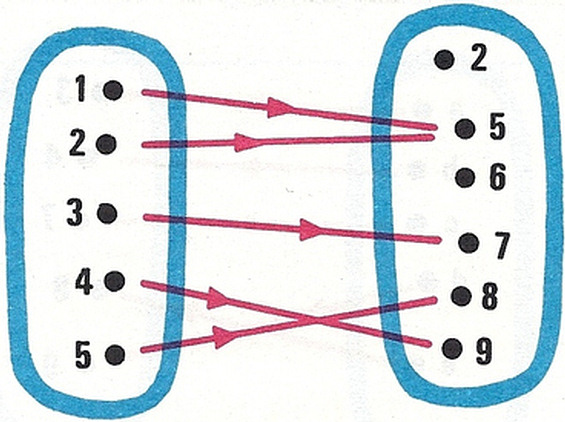
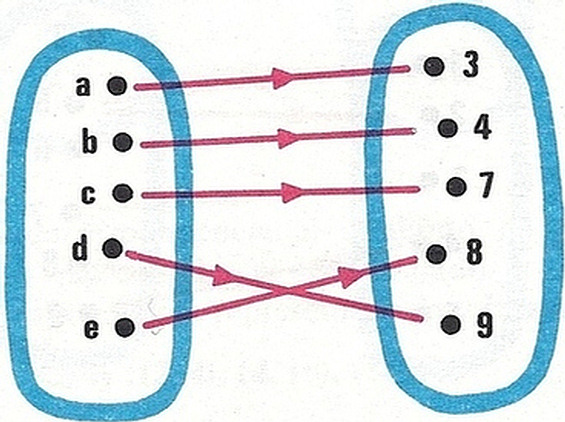
Una aplicación es la representada a continuación:

APLICACIONES INYECTIVA, SUPRAYECTIVA Y BIYECTIVA
Una aplicación entre dos conjuntos A y B es inyectiva cuando además de ser aplicación cumple la condición de que ningún elemento del conjunto final tiene más de un origen (uno o ninguno).

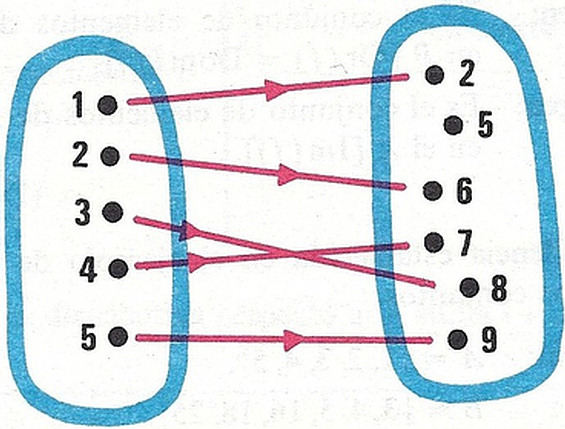
Una aplicación inyectiva es la siguiente:

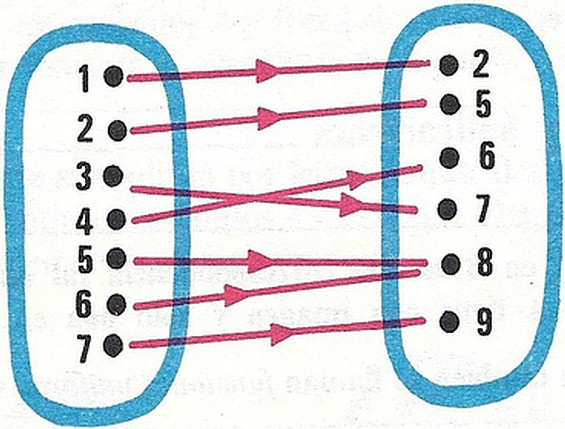
Una aplicación entre dos conjuntos A y B es suprayectiva cuando además de ser aplicación todos los elementos del conjunto final tienen algún origen (uno o más). Así:

Aplicación biyectiva entre dos conjuntos A y B es la aplicación que es a la vez inyectiva y suprayectiva. Por ejemplo:

•Cómo saber si he sido secuestrado por alienígenas. Pérdida de tiempo, terror irracional, alteraciones del sueño, hemorragias... Los investigadores de la abducción dicen que estos indicios son comunes en personas presuntamente secuestradas por alienígenas. Pero, cuidado, estos síntomas pueden indicar también problemas terrenos que requieran de atención médica.

•El viejo hombre de Shropshire. Uno de los casos más aceptados de longevidad inusual, incluso entre la comunidad científica, fue el del británico Thomas Parr, que decía tener 152 años en 1635. Considerada hoy día un mito, está enterrado en el Rincón de los Poetas de la Abadía de Westminster, al lado nada menos que de Shakespeare, Byron y Milton.

•El Triángulo de las Bermudas. Las desapariciones en el mar han sido numerosas y aun los casos no resueltos son generalmente explicables. Pero si existe un lugar donde las condiciones en que han sucedido estos dramas permanecen aún en la oscuridad, ese lugar es sin duda una extensa área geográfica situada entre las islas Bermudas, Puerto Rico y Florida.

•Experiencia cercana a la muerte. Sensación de atravesar un túnel, experiencia extracorpórea, visiones de luz, encuentros con personajes espirituales y amistades o parientes difuntos... Estos son algunos rasgos comunes de las ECM. Quienes lo han experimentado pierden el miedo a la muerte, se toman las cosas con más calma, serenidad y filosofía, son más felices.

MUY IMPORTANTE: Revista CAOS se define a sí misma como una web solidaria, es por ello que desinteresadamente deseamos lanzar una campaña de concienciación de nuestros corazones. Observamos con desasosiego que estamos perdiendo humanidad. Salvo en situaciones muy concretas de gran resonancia mediática, cada vez nos cuesta más mostrar afecto por el desconocido, ofrecer ayuda si a cambio no vamos a sacar una contrapartida por pequeña que esta sea… y resulta intolerable. No podemos hacer de este mundo algo tan horrible, tan egoísta, tan frío, tan falto de vida, por ello animamos a todo aquel que visita nuestra página a una reflexión sincera que le empuje a activarse y participar en alguna asociación de ámbito local que ayude a los más necesitados, a los faltos de recursos, ancianos, niños, discapacitados, enfermos terminales, que se preocupe por el cuidado del medioambiente, en contra de la crueldad con los animales… Y no hablamos sólo de dinero: dona ropa, sangre… levanta la vista, deja el teléfono móvil por un rato y ofrece tu tiempo, amistad, apego, conocimientos profesionales… No hacemos publicidad de ninguna entidad en concreto para que cada cual escoja aquella que le haga sentir más a gusto y de ese modo asuma la causa ajena como propia. Estamos seguros que si cada uno de nosotros pone un pequeño granito de arena en su entorno, todos juntos, por extensión, haremos de este planeta un lugar mejor, un rincón del cosmos donde realmente merezca la pena vivir; y de paso erradiquemos ese mal humor perpetuo, esa falta de educación y ausencia de empatía que inunda las calles de nuestros barrios y ciudades. En nombre de todas esas personas a las que a diario regalas lo mejor de ti mismo y la mayor de tus sonrisas, de corazón: muchas gracias.